
New research by Dr. Susu Zhang and a team of researchers provides fresh insights into when bifactor models—a popular statistical method used to explain psychological phenomena—will and will not generate unique results.
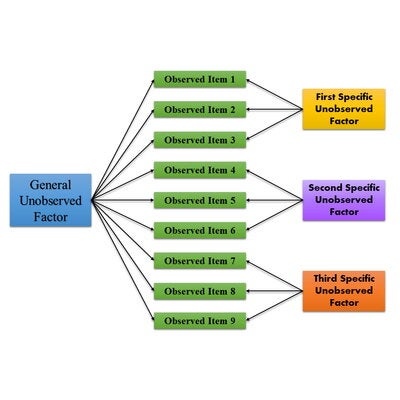
Psychologists often use a collection of items—survey questions, physiological measurements, ratings, or clinical observations— to measure psychological phenomena that can’t be observed directly. Bifactor models try to parcel how all of the items go together and how subsets of those same items increase or decrease together separately from other items. That is, they try to identify distinct factors among the items that vary together and correspond to the psychological phenomena under study. For example, anxiety and depression often co-occur and jointly might be part of a general factor of psychological distress, but each has distinct properties as well (the specific factors). Bifactor models try to determine how all of the items go together and how subsets of them vary separately as a way to better characterize the psychological phenomena.
Dr. Zhang and colleagues described the specific mathematical conditions necessary for bi-factor models to produce meaningful results. Bifactor models commonly suffer from a statistical problem called nonidentifiability: Testing the same model on the same data repeatedly doesn’t produce the same solution each time. For example, the model might sometimes show a strong relationship between anxiety and depression and other times a weak one, even if the data are unchanged (often, the result is what’s called “non-convergence”—the statistical software doesn’t report a single solution). When bifactor models are non-identifiable, researchers can’t draw clear conclusions about how the psychological phenomena are related.
Although bifactor models are widely used, they often are non-identifiable—multiple, equally good models can explain the same data, preventing scientists from drawing valid conclusions. Dr. Zhang and colleagues described a set of assumptions about how the observations are related that, when met, ensure that the bifactor model is unique and identifiable. They provide guidelines for when psychologists should, and more importantly, should not use the bifactor model, thereby helping researchers improve their understanding of important psychological phenomena.
This research was reported in:
Fang, G., Guo, J., Xu, X., Ying, Z., & Zhang, S. (2020). Identifiability of Bifactor models. Statistica Sinica. https://doi.org/10.5705/ss.202020.0386
This article originally published by the Illinois Department of Psychology